When it comes to a marriage with quantum theory, gravity is the lone holdout among the four fundamental forces in nature. The three others-the electromagnetic force, the weak force, which is responsible for radioactive decay, and the strong force, which binds neutrons and protons together within the atomic nucleus-have all merged with quantum theory to successfully describe the universe on the tiniest of scales, where the laws of quantum mechanics must play a leading role.
Although Einstein's theory of general relativity, which describes gravity as a curvature of space-time, explains a multitude of gravitational phenomena, it fails within the tiniest of volumes-the center of a black hole or the universe at its explosive birth, when it was less than an atomic diameter in size. That's where quantum mechanics ought to dominate.
Yet over the past eight decades, expert after expert, including Einstein, have been unable to unite quantum theory with gravity. So, is gravity truly a quantum force?
Researchers at the National Institute of Standards and Technology (NIST) and their colleagues have now proposed an experiment that may help settle the question.
S. Kelley/NIST
S. Kelley/NIST
S. Kelley/NIST
S. Kelley/NIST
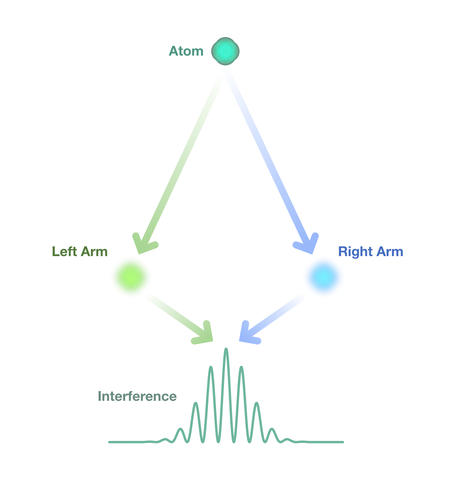
The experiment takes advantage of two of the weirdest properties of quantum theory. One is the superposition principle, which holds that an undisturbed atomic particle can be described as a wave, with some probability of being in two places at once. For instance, an undisturbed atom traveling through a region with two slits, passes through not one or the other of the slits but both. And because the atom is described by a wave, the portion that passes through one slit will interfere with the part that passes through the other, producing a well-known pattern of bright and dark fringes. The bright fringes correspond to regions where the hills and valleys of the two waves align so that they add together, creating constructive interference and the dark regions correspond to regions where the hills and valleys of the waves cancel each out, creating destructive interference.
The second strange quantum property is known as entanglement, a phenomenon in which two particles can be so strongly correlated that they behave as a single entity. Measuring a property of one of the particles automatically forces the other to have a complementary property, even if the two particles reside galaxies apart.
In a quantum theory of gravity, the gravitational attraction between two massive objects would be communicated by a hypothetical subatomic particle, the graviton, in the same way that the electromagnetic interaction between two charged particles is communicated by a photon (the fundamental particle of light). So, if a graviton truly exists, it should be able to connect, or entangle, the properties of two massive bodies, just as a photon can entangle the properties of two charged particles
The proposed experiment by Jake Taylor of NIST's Joint Quantum Institute at the University of Maryland, along with Daniel Carney, now at the Lawrence Berkeley National Laboratory, and Holger Müller of the University of California, Berkeley, provides a clever way to test if two massive bodies can indeed become entangled by gravity. They described their work in an article published online in Physical Review X Quantum on August 18, 2021.
The experiment would use a cold cloud of atoms, trapped inside an atomic interferometer. The interferometer has two arms-a left arm and a right. According to the superposition principle, if each atom in the cloud is in a pure, undisturbed quantum state, it can be described as a wave occupying both arms simultaneously. When the two portions of the wave, one from each arm, recombine, they will produce an interference pattern that reveals any changes to their paths due to forces like gravity.
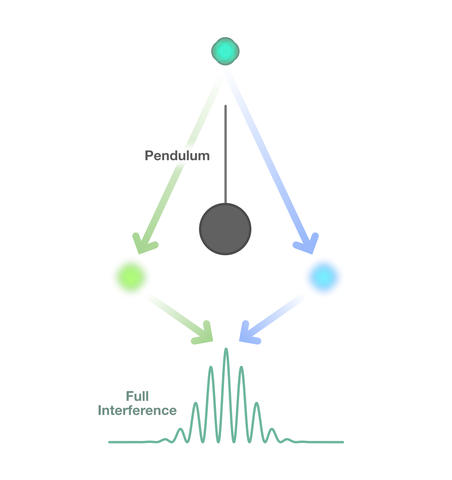
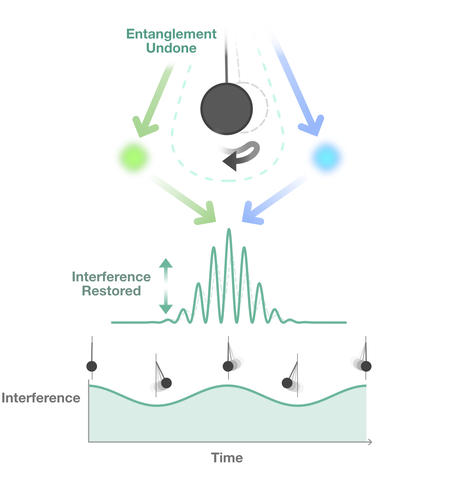
A small, initially stationary mass suspended as a pendulum is introduced just outside the interferometer. The suspended mass and the atom are gravitationally attracted. If that gravitational tug also produces entanglement, what would that look like?
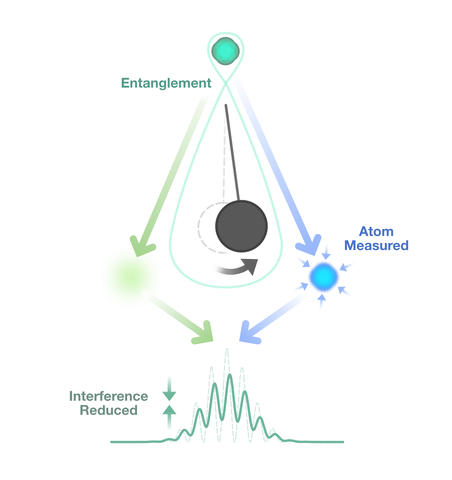
The suspended mass will become correlated with a specific location for the atom-either the right arm of the interferometer or the left. As a result, the mass will start swinging to the left or the right. If the atom is located on the left, the pendulum will start swinging to the left; if the atom is located on the right, the pendulum will start swinging to the right. Gravity has entangled the position of the atom in the interferometer with the direction in which the pendulum begins swinging.
The position entanglement means that the pendulum has effectively measured the location of the atom, pinpointing it to a particular site within the interferometer. Because the atom is no longer in a superposition of being in both arms at the same time, the interference pattern vanishes or diminishes.
Half a period later, when the swinging mass returns to its starting point, it loses all "memory" of the gravitational entanglement it had created. That's because regardless of what path the pendulum took--initially swinging to the right, which picks out a location for the atom in the right interferometer arm, or initially swinging to the left, which picks out a location for the atom in the left arm--it returns to the same starting position, much like a child on a swing. And when it returns to the starting position, it's equally likely that the pendulum will pick out a location for the atom in the left or right arm. At that moment, entanglement between the mass and the atom has been erased and the atomic interference pattern reappears.
Half a period after that, as the pendulum swings to one side or the other, entanglement is re-established and the interference pattern diminishes once again. As the pendulum swings back and forth the pattern repeats-interference, diminished interference, interference. This collapse and revival of interference, the scientists say, would be a "smoking gun" for entanglement.
"It is difficult for any phenomenon other than gravitational entanglement to produce such a cycle," said Carney.
Although the ideal experiment may be a decade or more from being built, a preliminary version could be ready in just a few years. A variety of shortcuts could be exploited to make things easier to observe, Taylor said. The biggest shortcut is to embrace the assumption, similar to Einstein's theory of general relativity, that it doesn't matter when you start the experiment - you should always get the same result.
Taylor noted that non-gravitational sources of quantum entanglement must be considered, which will require careful design and measurements to preclude.
Paper: Daniel Carney, Holger Müller, and Jacob M. Taylor. Using an atom interferometer to infer gravitational entanglement generation. Physical Review X Quantum, vol. 2, issue no. 3, 030330 published online Aug 18, 2021. DOI: https://doi.org/10.1103/PRXQuantum.2.030330