The Riemann hypothesis raised in 1859 is one of the six unsolved Millennium problems, and its proof greatly facilitate the understanding of the distribution laws of prime numbers. For a long time, there has been a growing academic focus on the non-trivial zeros of the Riemann zeta function. This enables physicists to reproduce prime numbers and inspires them to discover the essence of Riemann hypothesis with a feasible quantum approach.
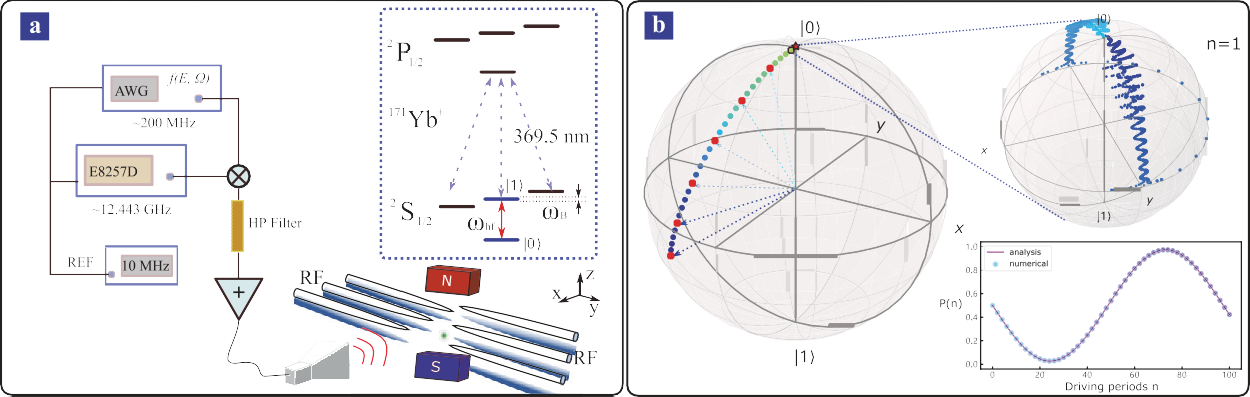
To achieve the high-precision measurement of the locations of the Riemann zeros, Prof. GUO Guangcan's research team from the University of Science and Technology of China (USTC) of the Chinese Academy of Sciences adopted a trapped ion system.
The team, together with Spanish theoretical physicists Prof. Charles Creffield and Prof. German Sierra, measured experimentally the first 80 Riemann zeros by using a trapped-ion qubit in a Paul trap, which is periodically driven with microwave fields. The results were published in NPJ Quantum Information on July 14.
Among all possible solutions, the Hilbert-Pólya conjecture combines the Riemann zeta function with quantum theory. The conjecture assumes the existence of a quantum system in which the eigenvalues of the Hamiltonian quantities are consistent with the Riemann zeros. Researchers are attracted by this conjecture and discover many potential static Hamiltonians. But these static Hamiltonians are difficult to measure experimentally.
In this work, the researchers chose not to prove the Riemann hypothesis, but to provide a physical embodiment of mathematical objects by using advanced quantum technology. In the trapped ion system, the ion was subjected to a time-periodic driving field, and its behavior was consequently described by Floquet theory. When an effect termed "coherent destruction of tunneling" appeared, they could observe the freezing of the qubit's dynamics as the driving parameters were varied.
Thanks to high-fidelity quantum operations and a long coherence time, the researchers achieved 30 driving periods and measured the first 80 Riemann zeros, an improvement of nearly two orders of magnitude over previous works.
This work provides an important experimental basis for researchers to study the Hilbert-Pólya conjecture and to gain a deeper understanding of the connection between the Riemann hypothesis and quantum systems.