A nearly 60-year-old mathematical problem has finally been solved.
The story began last fall when David Smith, a retired print technician from Yorkshire, England, came upon a shape with a tantalizing property. The life-long tiling enthusiast discovered a 13-sided shape - dubbed the hat - that is able to fill the infinite plane without overlaps or gaps in a pattern that not only never repeats but also never can be made to repeat.
This elusive shape is known to mathematicians as an aperiodic monotile or an einstein, a clever pun that takes its name from the German words ein and stein that mean one stone.
"Dave and I had been in touch over the years and we belong to the same old-fashioned listserv for people interested in tiling, a mix of tiling enthusiasts, programmers and mathematicians," recalls Cheriton School of Computer Science professor Craig S. Kaplan, who collaborated with Smith, software developer Joseph Myers and mathematician Chaim Goodman-Strauss on the paper that has proven that the elusive einstein exists.
"Dave was on to something big, something historic, but he hit the wall on what he could deduce about this shape by working with paper cut-outs. He knew I had recently published a paper about a related topic for which I developed a piece of software that we could use to understand what his shape was doing. He sent me an email asking, 'Hey, can you run this through your software and see what happens?'"

Professor Craig S. Kaplan holds two einstein tiles, a 13-sided shape he and his collaborators call the hat that can tile the plane indefinitely without the pattern ever repeating. Professor Kaplan is interested in a broad range of interdisciplinary topics, with a particular focus on interactions between mathematics and art. He uses mathematical ideas to create tools and algorithms that generate ornamental patterns and that empower artists and designers. His work incorporates knowledge from computer graphics, classical and computational geometry, human-computer interaction, graph theory, symmetry and tiling theory, and perceptual psychology.
Mathematicians had been trying to find a shape like David Smith's einstein since the 1960s when American mathematician Robert Berger discovered the first example of aperiodic tiling.
"Berger's aperiodic set of shapes was found in the mid-1960s and that set had 20,426 shapes," Professor Kaplan explained. "It was an elaborate construction with a combinatorial set of features that required a multiplicity of shapes to guarantee that the pattern doesn't repeat. That was an important discovery, but the natural next question for mathematicians is, can we get smaller sets? What's the lowest number of shapes we can do this with?"
By 1970, the set of shapes proven to tile aperiodically was down to about 100 and in 1971 mathematician Rafael Robinson got it down to six. Then, in 1974, Sir Roger Penrose discovered the eponymous Penrose tiles, which reduced the number to two.
"Those two shapes in Penrose's solution had enough structure that they forbid periodicity. But for almost 50 years mathematicians have been wondering, can we get down to just one shape? Can we do this with a monotile? That's the problem we solved. We found a single shape that does what all these earlier sets of multiple shapes are able to do."
In mathematics and computer science many problems remain open, but theoreticians have a strong sense what the answer will be even though a formal proof may be decades away.
"The famous P vs NP problem in computer science - a question about how long it takes to execute a particular class of algorithms - is still open, but there's a consensus how that's going to play out," Professor Kaplan said. "Almost every computer scientist thinks that P is not equal to NP. But the existence of an aperiodic monotile isn't in that category. Opinions were split. That's one of the things I love about this problem. It was not obviously true or obviously false. The only thing I knew for sure is that if it's false - if no aperiodic monotile exists - it would be extremely difficult to prove because that's a statement about all possible shapes. Whereas, proving that a particular shape is an aperiodic monotile is easier because, well, here it is. You're only trying to prove a property of a single shape."
Many have wondered if the hat - sometimes also called the shirt - has other tricks up its sleeve. In a sense it does.
"In our paper we show that the hat is not just a single shape that tiles aperiodically, but a member of a continuum of shapes. We can say that the hat is not the only aperiodic monotile, but it feels like a bit of a cop-out because all those shapes are closely related. They're one big family. The more interesting question is are there fundamentally different aperiodic monotiles? My answer is that there's no reason to suspect otherwise and every reason to suspect there ought to be others."
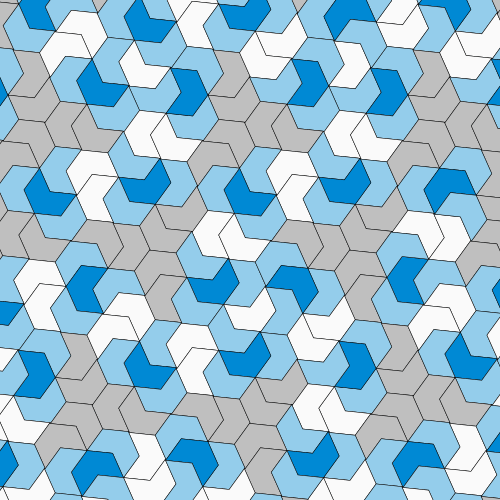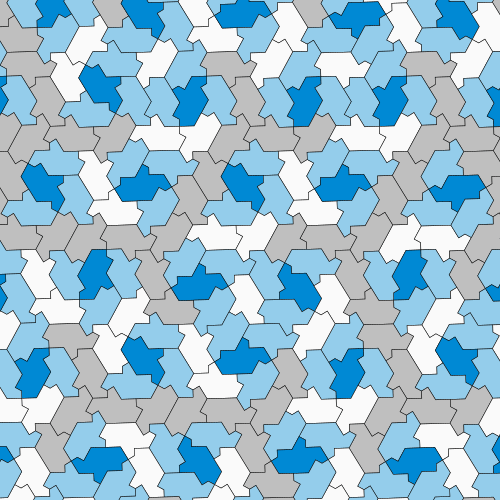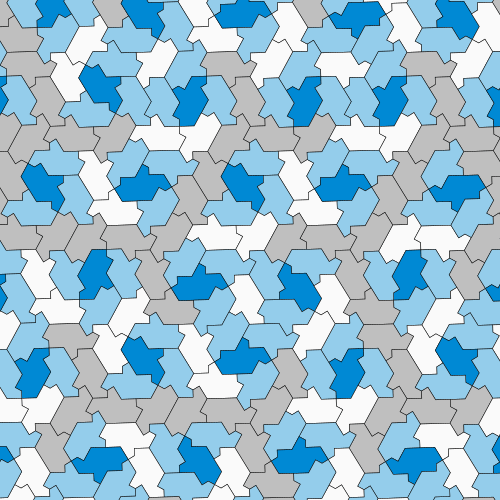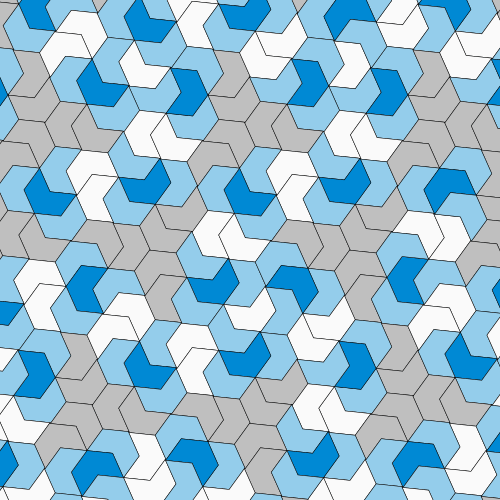
As shown in this looping animated GIF, the hat is one member of a continuous family of shapes that are all aperiodic, and that all tile the plane in the same way.
The main proof in the paper is combinatorial and benefits greatly from computer assistance, Professor Kaplan said. "It's combinatorial in that there are a few steps in the proof that depend on examining all the ways individual tiles can be next to each other and all the ways tiles can group together into larger and larger clumps. As it turns out, there are a lot of ways. Depending on what you're counting, it's dozens, hundreds, thousands."
You could grind through all of those cases tediously by hand, but if you have a computer science background so much the better. Why not write a piece of software to do that for you?
"The key computer-assisted part of our proof involves saying, 'We have to be able to say things about generic tilings of the hat that we don't know anything about.' But how can we say anything about a tiling whose structure we have no control over? In this part of the proof, we show that even though you didn't know anything going in, the tiling has a certain structure that you can account for. One way you can do that is to exhaustively enumerate little neighbourhoods of tiles - all the little neighbourhoods that possibly could occur in a real tiling."
A lot can be rejected. In one particular neighbourhood, you see there's no way to surround those tiles by another layer of tiles, so it couldn't occur in a real tiling. It's just an isolated blob.
"We can write a program to find all the ways you can have a little blob that is legally able to occur in a full tiling and we then wrote code that says something interesting about each of those different blobs that allows us to conclude that therefore an arbitrary tiling must have the properties we want it to have. The program we wrote confirms that those rules are followed in every possible tiling."
Penrose's tiles were found to have a deep connection to the natural world. In 1982, Iowa State University Professor Dan Shechtman discovered that symmetries similar to the ones in Penrose tiles are found in molecular structures called quasicrystals - a crystalline molecule that is ordered but not periodic - a discovery that led to his receiving the 2011 Nobel Prize in Chemistry.
"It's fun to speculate, but I'm not a physicist or an engineer," Professor Kaplan said. "That the Penrose tiling has a connection to materials science is amazing, but it's no guarantee that other aperiodic tilings do or that the hat will. My work is about the applications of mathematics in art. First and foremost, for me the hat tiling is interesting and it is visually arresting. People have already been using it to make interesting designs in different media. Please keep doing that. That's amazing and I love it."

An interpretation of the hat monotile, as gingerbread cookies. This tweet was one of many using different media to share the discovery.
Perhaps the hat could leave its mark at Waterloo in a more concrete way.
"There's a stone courtyard at the University of Oxford's Mathematical Institute where Penrose works that has been tiled with Penrose tiles. If you have a breakthrough in tiling theory, how are you not putting that on the floor of one of your academic buildings? The timing is nearly perfect now that the Math 4 building has been approved for construction and is in the design phase."






